jueves, 24 de abril de 2014
Formula para la curvatura Unidad 3
¿Cómo calculo la curvatura de una función vectorial en el espacio dado un punto de la curva?
r(t)= Ln(t)i + (t)j + (t^2) k
calcular la curvatura en el punto (0,1,1)
entonces si obtenemos la primera derivada es: r'(t)= (1/x) i+ j + (2t)k
y la segunda es : r''(t)= (-1/x^2) i + 0j + (2)k
la fórmula para calcular curvaturas en el espacio es
k= //T'(t)// dividido entre //r'(t)// o bien /V producto cruz con A/ entre la magnitud de la velocidad
Vector Tangente, Normal y Binormal Unidad 3
La tangente de una curva es una recta que
intersecta la curva en un solo punto. Es conocido por nosotros a través del
cálculo que mediante la diferenciación de una función se obtiene el punto
tangencial para la curva de esa función. Un concepto similar es aplicable al
cálculo vectorial, junto con una excepción.
Para una función con un vector de la forma, (x), un
vector de la forma es llamado vector tangente en el caso de que esta función
sea real y su magnitud no sea igual a cero. En esta situación, la tangente de
la función dada (x) en un punto arbitrario es paralela al vector tangente, en
ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito
esencial. Esto es debido a que un vector de magnitud cero no puede tener
dirección.
De manera similar, un vector tangencial unitario es
definido como,
Aquí s es la longitud total del arco dado, (t) es
el vector posición de la función dada y t es la variable de parametrización.
En la figura anterior, X es un punto estático,
mientras que P es un punto en movimiento. El punto P se mueve lentamente en la
dirección del punto X, mientras el punto P se acerca al punto X, el vector
desde el punto X hasta el punto P se acerca al vector tangente en el punto X.
La recta que contiene el vector tangente se conoce como recta tangencial.
Un vector normal es algo similar a un vector
unitario, suponga que para una función (x), (t) es el vector posición, entonces
el vector normal para la función dada es definida como,
Aquí es el vector unitario de la función dada.
Como se describió en la figura anterior, un vector
normal es un vector que está perpendicular a un plano o superficie dada. Un
vector normal para una superficie dada en un punto arbitrario,sea (x, y), está
dado por una matriz como la siguiente,
Aquí fx y fy son diferenciales parciales de la
función dada con respecto a x e y.
De la misma forma, el vector normal a un plano es
representado por una matriz como,
Donde la ecuación del plano es,
f(x, y, z) = ax
+ by + cz + d = 0
Un vector binormal es un producto cruz o producto
vectorial del vector normal y del vector unitario normal. Suponga que para una
función (x), (t) es el vector posición, entonces el vector binormal para la
función dada se define como,
Como sabemos que tanto un vector unitario como un
vector normal son vectores unitarios y que se encuentranperpendicular a la
superficie dada, un vector Binormal es también un vector unitario que se
encuentra normal a un plano o superficie dada. Este vector es normal a ambos,
el vector unitario y el vector normal.
Derivemos ahora el vector tangente, el vector
unitario y el vector normal para una funcióndeterminada.
(t) = <cos (t), sin (t), t>
(t) = ←sin (t), cos (t), 1>
=
=
= ←sin (t)/ , cos (t)/ , 1/
>
(t) = ←cos (t)/ , -sin (t)/ , 0>
(t)
|
=
|
= 1/
(t) = ←cos (t), -sin (t), 0>
= ←sin (t)/ , cos (t)/ , 1/ > X ←cos (t), -sin
(t), 0> = <sin (t)/ , -cos (t)/ , 1/ >
jueves, 10 de abril de 2014
Longitud de arco unidad 3
Cálculo mediante integrales
Al considerar una curva definida por una función 
y su respectiva derivada 
que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:
y su respectiva derivada que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:(1)
![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](http://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)
En el caso de una curva definida paramétricamente mediante dos funciones dependientes de t como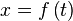 
e 
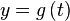, la longitud del arco desde el punto 
hasta el punto 
se calcula mediante:
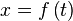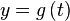e , la longitud del arco desde el punto hasta el punto se calcula mediante:(2)
![s = \int_{a}^{b} \sqrt{\left [ f' \left ( t \right ) \right ] ^2 + \left [ g' \left ( t \right ) \right ] ^2} \, dt](http://upload.wikimedia.org/math/8/4/8/8483f65e52e30ec4f0f24dfd8f6751a2.png)
Si la función está definida por coordenadas polares donde la coordenadas radial y el ángulo polar están relacionados mediante 
, la longitud del arco comprendido en el intervalo ![[\alpha, \beta] \,](http://upload.wikimedia.org/math/8/c/6/8c6ce103bd2dced02e71009e5e83dbe4.png)
, toma la forma:
, la longitud del arco comprendido en el intervalo , toma la forma:(3)
![s = \int_{\alpha}^{\beta} \sqrt{[ f (\theta)]^2 + \left [ f' (\theta) \right ] ^2} \, d \theta\](http://upload.wikimedia.org/math/4/8/0/480ba7ee65e91f33a5866602be9c3249.png)
Funciones hiperbolicas Unidad 3
FUNCIONES HIPERBÓLICAS
Las funciones y = sinh x, y = cosh x, y = tanh x.
En forma analítica, estas funciones pueden ser expresadas de forma análoga a las relaciones de Euler para las funciones circulares, esto es:
* gráfica de y = sinh x
| La función senh x crece muy rápidamente hacia infinito , tanto en el eje positivo como en el negativo (hacia infinito negativo). |
* gráfica de y = cosh x
| La función cosh x crece muy rápidamente tanto en el eje positivo como el negativo hacia infinito positivo. |
* gráfica de y = tanh x
| La función y = tanh x tiene por asíntota y=1 en el infinito positivo, y por asíntota y=-1 en el infinito negativo. |
Algunas relaciones:
Suscribirse a:
Entradas (Atom)