Cálculo mediante integrales
Al considerar una curva definida por una función 
y su respectiva derivada 
que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:
y su respectiva derivada que son continuas en un intervalo [a, b], la longitud s del arco delimitado por a y b es dada por la ecuación:(1)
![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](http://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)
En el caso de una curva definida paramétricamente mediante dos funciones dependientes de t como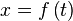 
e 
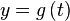, la longitud del arco desde el punto 
hasta el punto 
se calcula mediante:
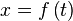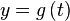e , la longitud del arco desde el punto hasta el punto se calcula mediante:(2)
![s = \int_{a}^{b} \sqrt{\left [ f' \left ( t \right ) \right ] ^2 + \left [ g' \left ( t \right ) \right ] ^2} \, dt](http://upload.wikimedia.org/math/8/4/8/8483f65e52e30ec4f0f24dfd8f6751a2.png)
Si la función está definida por coordenadas polares donde la coordenadas radial y el ángulo polar están relacionados mediante 
, la longitud del arco comprendido en el intervalo ![[\alpha, \beta] \,](http://upload.wikimedia.org/math/8/c/6/8c6ce103bd2dced02e71009e5e83dbe4.png)
, toma la forma:
, la longitud del arco comprendido en el intervalo , toma la forma:(3)
![s = \int_{\alpha}^{\beta} \sqrt{[ f (\theta)]^2 + \left [ f' (\theta) \right ] ^2} \, d \theta\](http://upload.wikimedia.org/math/4/8/0/480ba7ee65e91f33a5866602be9c3249.png)
No hay comentarios:
Publicar un comentario